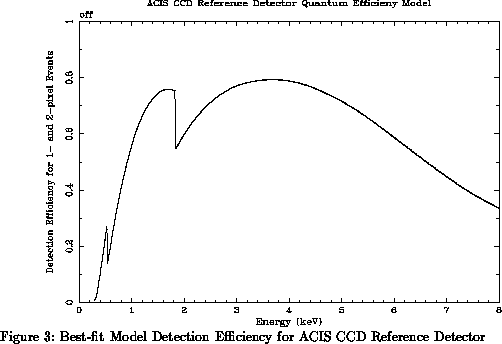
We measure the detection efficiency of the flight CCDs, relative to the synchrotron-calibrated standard detectors, using apparatus described by Jones et al. [5]. Briefly, both flight and reference detectors are illuminated by a quasi-monochromatic, temporally stable, diffuse (spatially uniform) X-ray beam of selectable energy. Since different physical processes are used to produce the X-rays at different energies, the spectral purity and spatial uniformity of the beam vary from energy to energy. Our use of CCD reference detectors, which have spectral and spatial resolution comparable to the flight devices being calibrated, allows us to measure and monitor the beam pattern and spectral content. This capability minimizes systematic errors resulting from non-ideal source characteristics.
Some statistics of the relative detection efficiency measurements
for one flight candidate detector (the same detector that was discussed in
section 4)
are shown in Table 4 for several energies. In this case,
the flight detector efficiency is slightly lower than that of the reference
detector at low energies; a reasonable fit to the low-energy (E< 3keV) data
is obtained if the silicon-dioxide deadlayer is
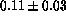microns thicker on the flight device than on the reference
detector.
Such a difference between the flight and reference detectors is
plausible,since the two detectors were produced in different lots
(the flight detector is serial number w201c3; the reference
detector is serial number w102c3). The flight
detector has higher efficiency than the reference detector at higher energies
because the flight detector is operated with higher bias than the reference.
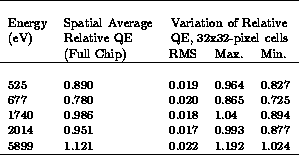
Table 4: Quantum Efficiency and Spatial Uniformity of an ACIS Flight CCD Relative to a CCD Reference Detector
Figure 8 illustrates the response uniformity of this flight
candidate detector at 5.9 keV; this variation is typical of what is observed at
other energies. Each pixel in the figure represents
the normalized detection efficiency of a 32-by-32 pixel cell in the CCD,
relative to the reference detector. Approximately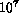 
photons
were detected in each detector at each incident energy; the contribution of
counting statistics to the relative error in each cell is 1.4%. (Ultimately
we hope to improve our knowledge of the beam pattern sufficiently that
the statistical error can be reduced to that contributed by the test detector
alone, viz., 1% per cell). The grayscale in the figure spans
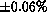, black-to-white, relative to the mean.
At all energies, the RMS fluctuation is about 2% on the scales shown in Figure 8. Note that statistical fluctuations of order 1.4% are expected in these data sets. Inspection of Figure 8 shows that the spectral variations are not randomly distributed over the detector. At this preliminary stage of analysis, we cannot rule out the possibility that there remain systematic errors, at the 1% level, in the flattening procedure. We believe we have demonstrated, however, that the detector response non-uniformity, over the spatial scales of interest, is at most of order 2%.
