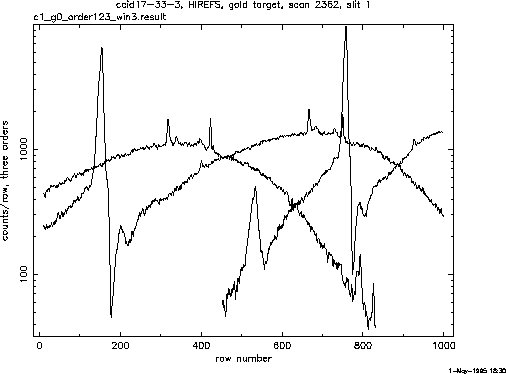
Figure 3: Intensity as a function of row number for three orders of the spectrometer with a gold target in the X-ray source.
Counting all the counts in each row of the CCD separately for each order of the spectrometer, and plotting intensity as a function of row number a Fig. 3 was produced, where three first orders are shown.
Fig. 3 shows a result of order separation, or, in other words, plots of intensity as a function of CCD row number for the first three orders of the spectrometer.

Figure 3: Intensity as a function of row number for three orders of the spectrometer with a gold target in the X-ray source.
A number of emission lines can be clearly seen in the spectrum,
as well as a very clear absorption edge (presumably, oxygen edge).
To convert the results into the energy scale one has to set a
correspondence between row number and an energy of the incoming beam.
This can be done by solving grating equation and identification at
least some known emission lines. On Fig. 4 is schematically shown
a geometry of the output stage of the spectrometer and a CCD. Input
X-ray beam hits reflecting grating at an angle  and, after
being dispersed, a component of wavelength
and, after
being dispersed, a component of wavelength 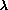 illuminates
a vertical plane of the CCD at the row x.
Angle
illuminates
a vertical plane of the CCD at the row x.
Angle 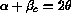 is fixed
by the spectrometer geometry and according to the manual
is fixed
by the spectrometer geometry and according to the manual 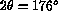 .
.
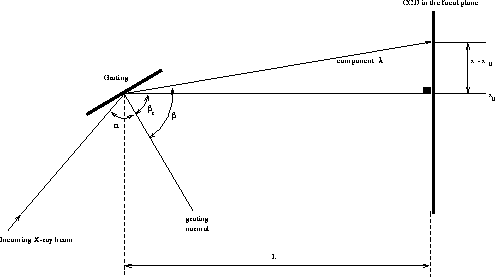
Figure 4: Geometry of light path between the grating and the CCD in the focal plane.
From Fig. 4 it is clear that
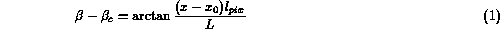
where 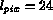 microns is CCD pixel size, L is a distance from the
grating to the focal plane.
From standard grating equation we have:
microns is CCD pixel size, L is a distance from the
grating to the focal plane.
From standard grating equation we have:

Here m is an order number, d is a grating period (208333 Angstroms).
Converting wavelength 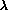 (in Angstroms) into energy E (in keV) with a
formula
(in Angstroms) into energy E (in keV) with a
formula

and combining (1) and (2), we get an equation that determines an energy of the incoming beam as a function of the row number of the CCD:
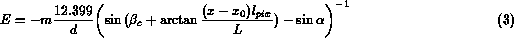
Angles  and
and 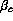 are defined by a geometry of the HIREFS,
and if the spectrometer is properly calibrated, according to the manual
are defined by a geometry of the HIREFS,
and if the spectrometer is properly calibrated, according to the manual
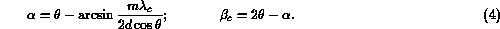
Here 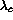 is reading of the wavelength counter of the spectrometer
in Angstroms, it corresponds to the first order wavelength, hitting CCD
at the row
is reading of the wavelength counter of the spectrometer
in Angstroms, it corresponds to the first order wavelength, hitting CCD
at the row 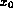 .
.
To set a precise energy scale we use several emission lines with known
energies, namely, carbon 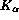 , nitrogen
, nitrogen 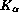 , and
oxygen
, and
oxygen 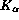 lines. Both first and second order oxygen line
are used in this calibration procedure. The least square fit to the relation
(3) with
lines. Both first and second order oxygen line
are used in this calibration procedure. The least square fit to the relation
(3) with 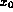 and L as free parameters at the emission line energies
is usually fairly robust. We found that the value of L
produced by fitting routine can be used to adjust the distance between the
grating and the
CCD, if it is out of the focal point. It is the most precise way to
measure this distance and
focus the instrument.
and L as free parameters at the emission line energies
is usually fairly robust. We found that the value of L
produced by fitting routine can be used to adjust the distance between the
grating and the
CCD, if it is out of the focal point. It is the most precise way to
measure this distance and
focus the instrument.
Equation (3) allows to determine a resolving power of the apparatus for any given energy, corresponding plot is shown at Fig. 5.
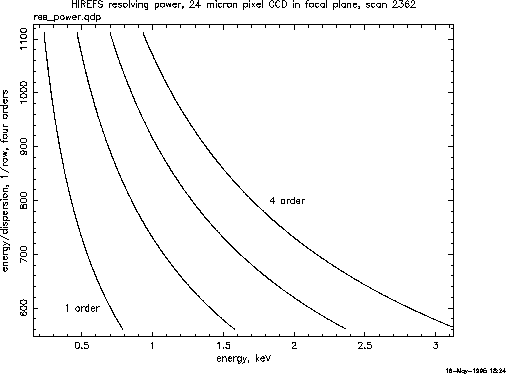
Figure 5: Spectrometer resolving power 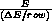 as a function of energy.
as a function of energy.
Resolving power R here is defined as a relative difference in energy
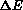 seen by two
adjacent rows of a CCD:
seen by two
adjacent rows of a CCD:

. For the interval of interest from 0.2 keV and up to 2 keV R changes roughly from 1000 to 500.